What is Eigenvalues and Eigenvectors?
Eigenvectors are unit vectors with length/magnitude is equal to 1. These are special vectors, given a transformation matrix M.
Eigenvalues are coefficients applied to eigenvectors that give the vectors their length or magnitude.
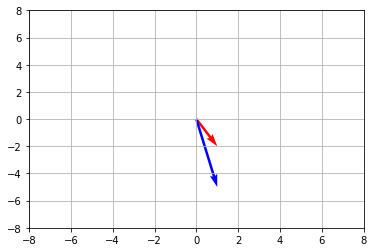
The eigenvalue is a scalar that is used to transform the eigenvector.
Ax = λx where “λ” is an eigenvalue of A.
Detailed math behind can be read here, the simplified explanation can be found here
The purpose of this post is to discuss where eigenvalues & eigenvectors are used in machine learning. The simple explanation is whenever we are dealing with large dimensions and huge data points, eigenvalues and eigenvectors can be used to transform the data into the most relevant dimensions which is the principal component to reduce the computation complexity involved without degrading the quality of data.
- Principle component analysis (PCA)
- Corner detection in computer vision
- Data Science
are some of the main areas where eigenvalues & eigenvectors getting used.
Linear Transformation
Linear transformation helps to transform from one vector space to another without changing the underlying structure of the vector spaces. It is very much important and useful because of vector space structure preservation.
Examples – Scaling , Translation , Rotation
Convolution is also a linear transformation
Linear Transformation Function F(vector) = M * vectorTo reduce the transformation complexity , vectors can be represented as a linear combination of Eigen vectors Code reference
How to find Eigen Vectors
Mx = c * x= (M-c*I)= Det(M-c*I) –> which solves cput the value of c in Mx = c*x x is the eigervectors and constant c is called eigenvalues for the linear transformation of M.
Calculating Eigenvalues and Eigenvectors with Numpy linear algebra API
from numpy import linalg as LA
M = np.array([[5,2],[3,4]])
lam,vec = LA.eig(M)
u = vec[:,1]
lam1 = lam[1]
print(" M.u= ",np.dot(M,u))
print("lam1.u= ",lam1*u)
M.u= [-1.10940039 1.66410059]
lam1.u= [-1.10940039 1.66410059]
Reconstruction of the matrix from eigen values and eigen vectors, we follow below code
from numpy.linalg import inv
# find inverse of eigenvector
R = inv(vec)
# find diagonal matrix from eigenvalues
D = np.diag(lam)
# reconstruct the original matrix
B = vec.dot(D).dot(R)
print("B =",B)
print("M =",M)
B = [[5. 2.]
[3. 4.]]
M = [[5 2]
[3 4]]
Thank you for the explanation
Realtime explanation with relevant example.